Veja como realizar cálculo de juros compostos no Excel passo-a-passo.
1. INTRODUÇÃO
Juros compostos representam juros sobre juros, sendo calculados sempre em relação ao valor anterior. Por este motivo, ao passar do tempo, os juros compostos representam maior crescimento quando comparados com os juros simples. A sua natureza exponencial ajuda a explicar o resultado dos rendimentos e fica evidenciada na fórmula exposta no tópico seguinte.
2. FÓRMULA DOS JUROS COMPOSTOS EXCEL
A fórmula matemática que rege os juros compostos, amplamente utilizada em matemática financeira, é:
M = C x (1 + i)n
Sendo:
- M = montante, que é o valor resultante ao final do período
- C = capital, que é o valor inicial (investido)
- i = taxa de juros, que é o percentual cobrado sobre o capital (C) a cada período de tempo (n)
- n = tempo, que é o número de períodos em que o capital (C) será aplicado
É importante ressaltar que a taxa de juros e o tempo precisam estar na mesma unidade. Caso a taxa seja, por exemplo, 1,2% ao mês (a.m), o número de períodos deverá ser também mensal. Caso a taxa seja anual, o número de períodos deverá ser também mensal. Isso implica fazer muitas vezes conversões para padronizar a unidade, convertendo para uma nova taxa de juros equivalente (como por exemplo: período de 2 anos e taxa de juros de 1,5% ao mês).
3. COMO CALCULAR JUROS COMPOSTOS NO EXCEL
Para calcular o montante no Excel podemos usar a função VF (valor futuro). Esta função possui 5 argumentos, sendo os 3 primeiros obrigatórios e os 2 últimos opcionais (note que argumentos opcionais aparecem entre colchetes no indicativo da sintaxe da função). A imagem a seguir exibe a sintaxe da função VF.
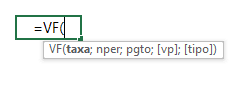
Sendo:
- taxa = taxa de juros vigente por período
- nper = número total de períodos
- pgto = pagamentos realizados (aportes que ajudam a somar ao montante, ou retiradas)
- vp = valor presente, que representa o capital
- tipo = especifica se os pagamentos são feitos no início ou no final de cada período (usa-se zero para definir que o fluxo de caixa é no final e 1 para definir que o fluxo de caixa é no início, sendo 0 o valor padrão, que é admitido caso o argumento seja omitido).
Caso optemos por não informar o valor presente, torna-se obrigatório informar os pagamentos, uma vez que sem ambos não haveria valorização que pudesse resultar em um montante positivo. Dado um certo valor presente informado, torna-se optativo especificar pagamentos a cada período visto que o capital inicial já será suficiente para gerar um montante ao passar dos períodos.
4. EXEMPLOS PRÁTICOS COM A FUNÇÃO VF
a) Com capital inicial e sem aportes (pagamentos)
A imagem a seguir exibe o cálculo do montante a partir de um valor inicial de R$ 2.000,00 (valor destacado em amarelo) associado a uma taxa de juros de 3,0% (pode ser mensal, ou anual, por exemplo) no decorrer de 12 períodos (pode ser mensal, ou anual, por exemplo). Note que optamos por especificar que não haverá pagamentos realizados (valor zerado destacado em cinza).

Note que o resultado apresenta valor negativo. Isso ocorre porque o capital (em C4), ao representar um desembolso, deveria estar com sinal negativo. Outro ajuste que pode ser realizado para a exibição do valor correto do montante é acrescentar o sinal de subtração antes da abertura da função (vide imagem a seguir).

Caso não tivéssemos disponível a célula C6 com o valor zerado para os pagamentos e mesmo assim desejássemos determiná-lo como zero, poderíamos preencher o argumento pgto com valor zero ou ainda omitir este argumento. Com isso teríamos fórmulas equivalentes e igualmente funcionais: =-VF(C5;C7;0;C4) ou =-VF(C5;C7;;C4). Esta segunda fórmula apresenta a omissão do argumento (note dupla ocorrência sequencial de ;).
b) Com capital inicial e com aportes (pagamentos)
O mesmo exemplo supracitado apresentará valor diferente (e maior, destacado em azul) caso optemos por fazer aportes a cada período como forma de contribuir para elevar o montante. A imagem a seguir considera que estamos injetando R$ 100,00 a cada período (valor destacado em cinza).

c) Sem capital inicial e com aportes (pagamentos)
Outra possibilidade é iniciarmos sem capital (valor zero, destacado em amarelo). Desta maneira torna-se obrigatório o fluxo de pagamentos a cada período (valor destacado em cinza).

5. ANÁLISE COMPARATIVA DOS 3 CENÁRIOS APRESENTADOS
Nota-se que dentre os 3 cenários expostos, aquele que representa o maior montante é o cenário no qual partimos de um valor inicial e também fazemos pagamentos a cada período.
O cenário que representa o menor montante é aquele em que não há capital inicial e todo o rendimento é baseado apenas nos pagamentos mensais. A tabela a seguir mostra o comparativo entre os 3 cenários.
A diferença entre os cenários 2 e 1 é justamente o valor do montante do cenário 3. Em outras palavras, os valores dos cenários 1 e 3 somados resultam no valor apresentado no cenário 2 (2.851,52 + 1.419,20 = 4.270,72), o que evidencia a equivalência dada a sua complementaridade.

6. CÁLCULO ALTERNATIVO AO USO DA FUNÇÃO VF
Podemos ainda chegar ao mesmo resultado sem empregar a função VF. A fórmula a seguir é a reprodução literal da fórmula citada na seção 2.

Download Planilha de Juros Compostos Excel
Realize o download da planilha de exemplo neste botão abaixo. Basta se inscrever na nossa newsletter gratuita para o download automático.
Curso Excel Completo – Do Básico ao VBA
Quer aprender Excel do Básico, passando pela Avançado e chegando no VBA? Clique na imagem abaixo:

